Pascal's Triangle
One of the coolest and most useful pieces of mathematics that you learn in high school math is what we call Pascal's Triangle. I've copied a few rows of the triangle below:

If you don't know how to form the values in the hexagons of this triangular shape, you'll want to look that up and explain it in your blog.
A couple of the interesting things include the following.
Find the sums of each row. Then compare these numbers. What pattern is represented?
The powers of 11 are represented in this triangle; how so? Use the triangle to find the seventh power of 11. Explain how you've done this.
Triangular numbers, square numbers, Fibbonacci numbers, prime numbers.....all appear in interesting patterns in Pascal's triangle. This interesting site will give you a simple introduction.
There's also some amazing visual patterns that appear in Pascal's triangle. Explore those and report back what you find. (I know there are some artsy folks out there -- this part's for you.)
In your blog this time, write something about Pascal's triangle. You can be expansive. Perhaps you'd like to write about how the Chinese people knew and used this triangle long before Pascal was born. Perhaps you'd like to write about Blaise Pascal himself: when did he live and what influences did he have? Of course it would also be wonderful for you to find something new and cool about the number patterns Pascal's Triangle.
Have fun. And. If you find some good piece of math humor, feel free to include that, too.
If you don't know how to form the values in the hexagons of this triangular shape, you'll want to look that up and explain it in your blog.
A couple of the interesting things include the following.
Find the sums of each row. Then compare these numbers. What pattern is represented?
The powers of 11 are represented in this triangle; how so? Use the triangle to find the seventh power of 11. Explain how you've done this.
Triangular numbers, square numbers, Fibbonacci numbers, prime numbers.....all appear in interesting patterns in Pascal's triangle. This interesting site will give you a simple introduction.
There's also some amazing visual patterns that appear in Pascal's triangle. Explore those and report back what you find. (I know there are some artsy folks out there -- this part's for you.)
In your blog this time, write something about Pascal's triangle. You can be expansive. Perhaps you'd like to write about how the Chinese people knew and used this triangle long before Pascal was born. Perhaps you'd like to write about Blaise Pascal himself: when did he live and what influences did he have? Of course it would also be wonderful for you to find something new and cool about the number patterns Pascal's Triangle.
Have fun. And. If you find some good piece of math humor, feel free to include that, too.
_________________________________________________________________________________
To get each value in the hexagons you must add the two above. For example the 4 in Row 4 comes from the one and three added together.
http://www.mathsisfun.com/pascals-triangle.html
Row Sum of Values in Hexagons
|
Row 1
|
1
|
|
Row 2
|
2
|
|
Row 3
|
4
|
|
Row 4
|
8
|
|
Row 5
|
32
|
|
Row 6
|
64
|
|
Row 7
|
128
|
|
Row 8
|
256
|
|
Row 9
|
512
|
|
Row 10
|
1024
|
|
Row 11
|
2048
|
|
Row 12
|
4096
|
|
Row 13
|
8192
|
The values of the hexagons in each row is equal to 2 to the power of the number of the row.
The powers of 11 are also shown, you just have to read it diagonally. But when there is multiple digits you would sometimes have to carry a digit over. For example the 7th row shows the numbers 1, 7, 21, 35, 35, 35, 21, 7, 1. 11 to the 7th power is 19487171. The 7 and 2 in twenty one combined to make nine, The 1 in twenty one combined with the 3 in thirty five to get four, and so on.
A new pattern I have discovered in Pascal's Triangle is that a number squared is equal to the number to right and the one below it added together.,
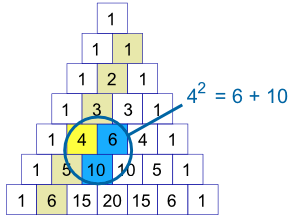
http://www.mathsisfun.com/pascals-triangle.html
Pascal was not the first to discover this triangle. A Chinese mathematician, Chia Hsein, in the 11th century used this to “was using the triangle to extract square and cube roots of numbers” (Clawson 133). http://pages.csam.montclair.edu/~kazimir/history.html

http://www.ualr.edu/lasmoller/pascalstriangle.html

http://www.quickmeme.com/Math-Major-Sloth/page/10/